Speaker: Camilo Andres Angulo Santacruz, Universidade Federal Fluminense

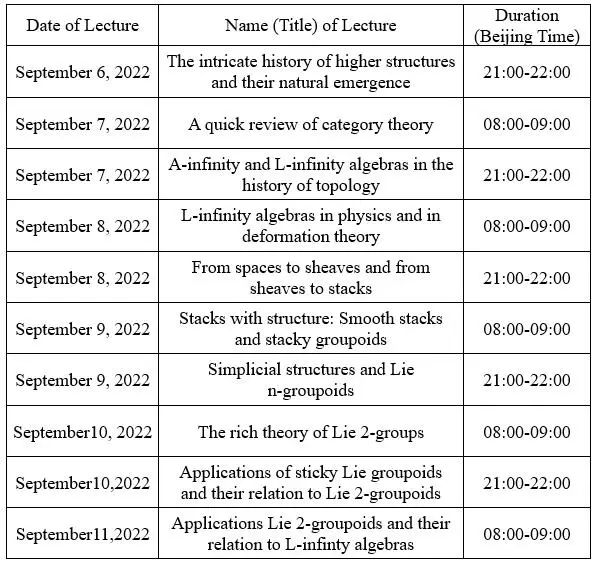
Time: September 6-11, 2022, GMT+8


Venue: Zoom Meeting ID ID：862 062 0549  Password：2022

Abstract:

“Higher structure” is a term used loosely to refer to a large collection of structures that share a common theme. Suppose a mathematical structure consists of a collection of sets, functions between them, and some equations that the latter shall verify. Think of group structures, for instance, as the sets G, GxG, and the singleton, together with three functions (the multiplication, the unit, and the inverse) that verify the usual axioms of a group, which are equations relating them(!). The common idea behind higher structures is that they roughly are like mathematical structures, but replacing sets by homotopy types, equations by homotopies, and adding higher-order homotopies to enforce coherence.

Higher structures have an intricate history and abound in mathematics. We will focus on three types of higher structures that have algebraic flavor.In what follows we describe the plan of the lectures. We will start by giving a bit of a panoramic perspective on the history and emergence of the higher structures we will consider. After going through some preliminaries, we proceed to study them one by one, starting with the so-called L-infinity algebras, continuing with stacky groupoids, and closing with Lie n-groupoids. In each module, we go through definitions, examples, and main constructions. We conclude by trying and relating these structures among them and by giving an outlook for the directions in which these generalize by touching upon some recent research topics.

Bipgraphy:

Camilo Andres Angulo Santacruz is a post doctor from Universidade Federal Fluminense, Brazil. He mainly study Poisson geometry and higher structures.

Source: SRMC