Peking University, December 14, 2023: Recently, a research team led by Prof. Sun Zhong at Peking University reported an analog hardware solution for real-time compressed sensing recovery, which has been published as an article titled "In-memory analog solution of compressed sensing recovery in one step" in Science Advances. In this work, a design based on a resistive memory (also known as memristor) array for performing instantaneous matrix-matrix-vector multiplication (MMVM) is first introduced. Based on this module, then an analog matrix computing circuit that solves compressed sensing (CS) recovery in one step (within few microseconds) is disclosed. 

CS has been the cornerstone of modern signal and image processing, across many important fields such as medical imaging, wireless communications, object tracking, and single-pixel cameras. In CS, sparse signals can be highly undersampled in the front-end sensor, which breaks through the Nyquist rate and thus significantly improving sampling efficiency. In the back-end processor, the original signals can be faithfully reconstructed by solving a sparse approximation problem. However, the CS recovery algorithm is usually very complicated and involves high-complexity matrix-matrix operations and pointwise nonlinear functions. As a result, CS recovery in the back-end processor has become the accepted bottleneck in the CS pipeline, which prevents its application in high-speed, real-time signal processing scenarios.

To speed up the CS recovery computation, there have been two lines of efforts in the traditional digital domain, using either advanced algorithms (e.g., deep learning), or parallel processors (e.g., GPU, FPGA and ASIC). However, the computing efficiency is fundamentally limited by the polynomial complexity of matrix operations in digital processors. To this end, analog computing has been regarded as an efficient approach for accelerating CS recovery, thanks to its inherent computational parallelism. Nevertheless, again, due to the high complexity of CS recovery algorithms, previous analog computing solutions either rely on pre-calculated matrix-matrix multiplication which is of a cubic complexity, or bare the discrete iterative process that requires expensive while frequent analog-digital conversions. Therefore, solving CS recovery in one step remains a grand challenge.
 

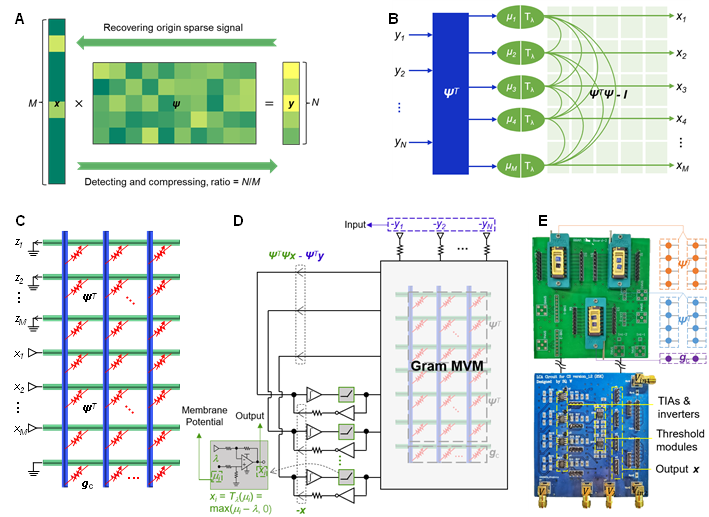
Fig. 1. The design of MMVM and LCA circuits.

In order to solve this problem, the team from Peking University first designed an analog in-memory computing module that implements MMVM in one step, thus avoiding the pre-calculation of matrix-matrix multiplication. By connecting this MMVM module with other analog components to form a feedback loop, the resulting circuit maps accurately the local competitive algorithm (LCA), which solves CS recovery in one step without discrete iterations. To validate the circuit, the team fabricated a resistive memory array with a standard semiconductor process, based on which the LCA circuit was constructed on a PCB for performing CS recovery. The compressed data was converted as input voltage signals in the circuit, and the recovered signals were acquired in a continuous-time manner. With this circuit, recovery of 1D sparse signals, 2D natural RGB images and magnetic resonance images (MRI) have been demonstrated in experiments. The normalized mean square error (NMSE) is around 0.01, and the peak signal-to-noise ratio (PSNR) of the images is 27 dB. The speed of this circuit is estimated to be 1-2 orders of magnitude faster than traditional digital approaches such as deep learning, and is also better than other electronic or photonic analog computing solutions. The circuit is highly promising to be implemented in the back-end CS processor to deliver real-time processing capability in the microsecond regime, which might in turn enable advanced medical, visual and communication techniques.

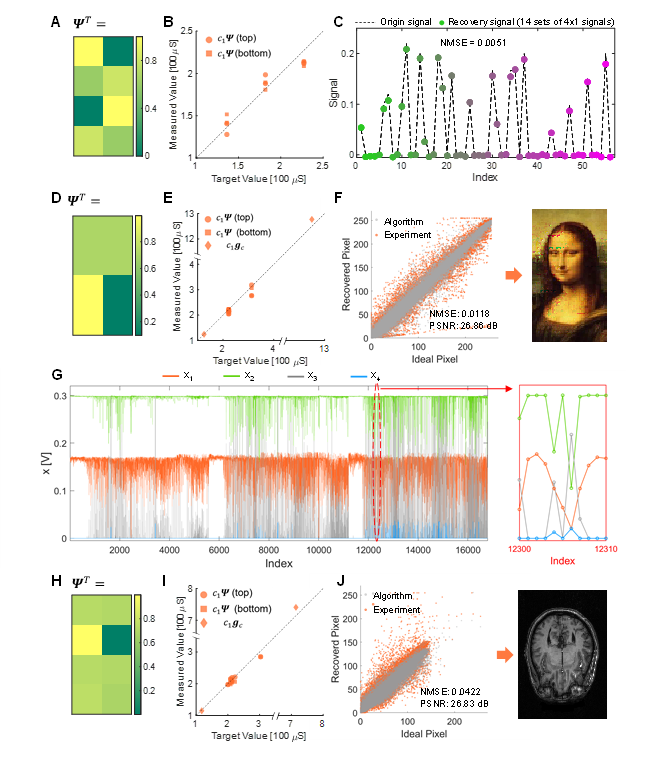
Fig. 2. Experimental results for recovering 1D sparse signal, 2D natural image and MRI.

Source: School of Electronics Engineering and Computer Science